Weird Stuff in High Dimensions
Tamanna Hossain-Kay / 2021-11-28
We’re usually putzing around in a dimensional space, perceiving the dimension of time as something we’re moving forward through. Attempts to explain our reality, however, have intriguingly and disturbingly given rise to the possibility of higher dimensions. Superstring Theory, for example, posits dimensions to provide a unifying framework between general relativity and quantum mechanics. M-Theory, on the other hand, posits dimensions, and Bosonic String Theory a daunting dimensions! In machine learning we work in even higher dimensions to model data. For example, Google’s BERT projects words on to or dimensional spaces in order to model human language.
What do these higher dimensions “look like”? The short answer is that to beings such as ourselves, i.e., mostly with some limited perception: very weird! Visualizing these higher dimensions in the traditional sense doesn’t seem possible for us, but we can still get insight into these spaces through mathematics. Frustratingly, many of these insights break from our usual or intuitions. As Thomas Banchoff wrote, “All of us are slaves to the prejudices of our own dimension.”
Read on to mathematically “see” some weird stuff in high dimensions.
Sources: This post is compiled using notes from CMU, Cornell, and UC Davis with some additional figures and exposition for my own understanding.
Warmup
Consider a dimensional unit square. If were to place points inside the square such that each coordinate for each point is drawn uniformly at random from the interval [0,1], what can we say about the distribution of distances between points?
Our usual intuition might be that the points will be spread out somewhat evenly. This holds true in our familiar and spaces. However, something different happens in higher dimensions.
Consider that the distance between any two points and is defined as ,
where for each dimension ,
Then are i.i.d random variables for all , and is a summation of independent random variables.
So in high dimensions, the Law of Large Numbers applies and converges to its expected value. The distances are then concentrated around a mean! However, in lower dimensions (like the 2D and 3D we’re perceptually accustomed to), is pre-convergence and the distances are still spread out.
Sphere
Consider a dimensional sphere of unit radius centered at the origin:
Compute surface area and volume
Volume goes to zero
Volume is near the equator
Volume is a narrow annulus
Compute surface area and volume
The surface area and the volume of a unit-radius sphere in dimensions are given by where is the Gamma functions.
Proof
Cartesian Coordinates
First, lets recall that in 3-dimensions a sphere of radius is defined as . In order to compute its volume we consider the region .
- Solving for gives:
- The projection of the sphere onto the plane when is the circle . Then solving for within the desired region gives:
Thus, the volume of the sphere can be computed as:
Extending this formula to a -dimensional sphere of radius 1 gives:
Polar Coordinates
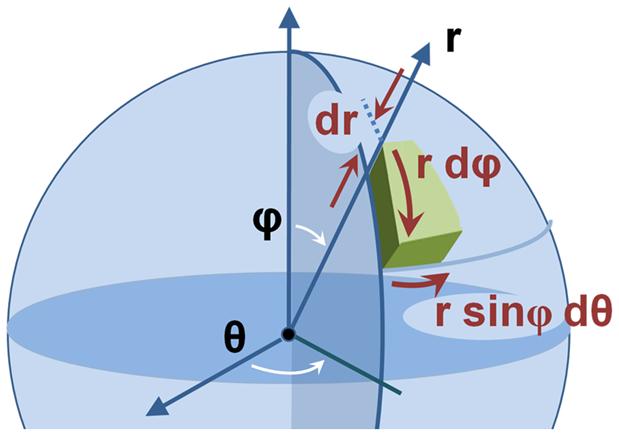
In 3-dimensions, a sphere of radius is defined as all points where , , and . Then the volume of the sphere can be computed as,
Using the concept of a solid angle to further simplify the integral by allowing us to write it over a coordinate free ‘direction’. Let be the surface area of the infinitismal piece of the solid angle of the sphere.
Then,
Extending this formula to a d-dimensional sphere of unit radius gives:
A Trick
Consider a different problem:
This can be computed in both Cartesian and Polar coordinates. They will be equated to solve our problem.
Cartesian: Polar: .
Then by equating the solution for in cartesian and polar coordinates,
Finally, using equation ,
More generally, the surface area and volume equations for a sphere of radius are,
Volume goes to zero
So, the denominator of grows faster than its numerator since grows much faster than ,. Thus,
Volume is near the equator
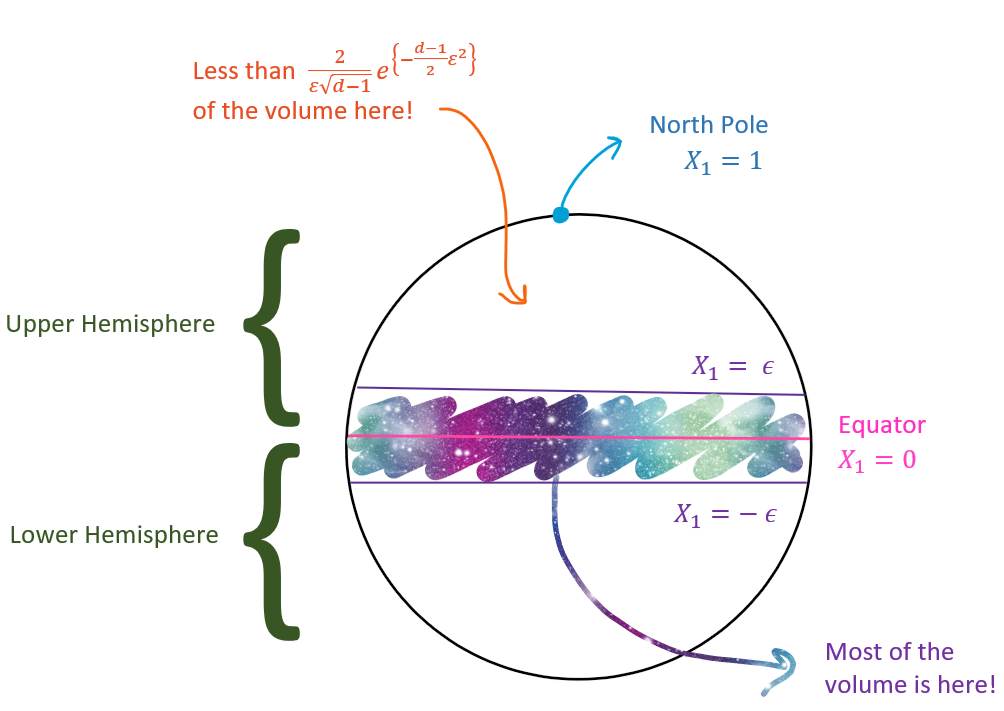
Without loss of generality, pick any of the poles of the sphere as the North Pole, say the pole along . Then the North Pole is .
Define the equator as the dimensional sphere: . This is formed by the intersection of the plane with the sphere. It has volume . Note that, in 3-dimensions this is (familiarly) a circle.
The equator divides the sphere into two hemispheres, or -dimensional half spheres, one upper and one lower.
Consider a plane slightly above the plane, for some . Less than fraction of the volume in the upper hemisphere lies above the plane. This value drops exponentially with as increases and goes to infinity. Same is true for volume below in the lower hemisphere.
Proof
Without loss of generality we will show the bound for the upper hemisphere.
Define the region as the portion of the sphere above the plane: . Then,
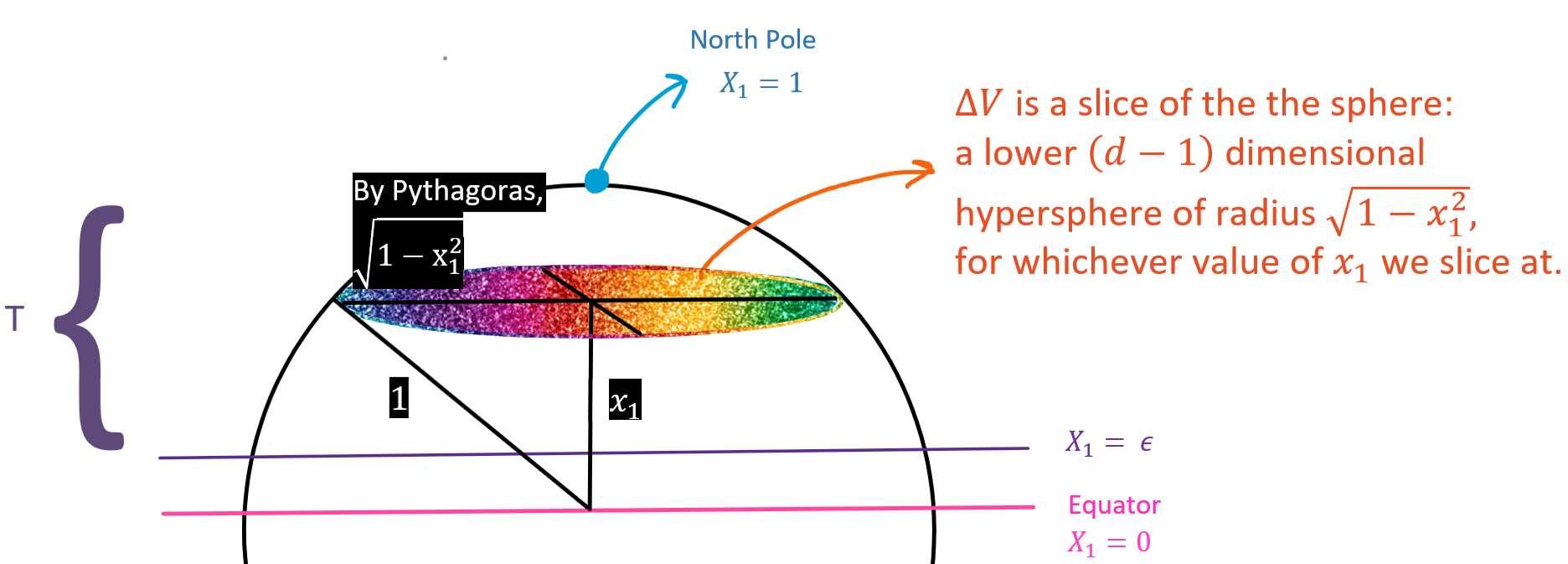
Thus,
Volume is a narrow annulus
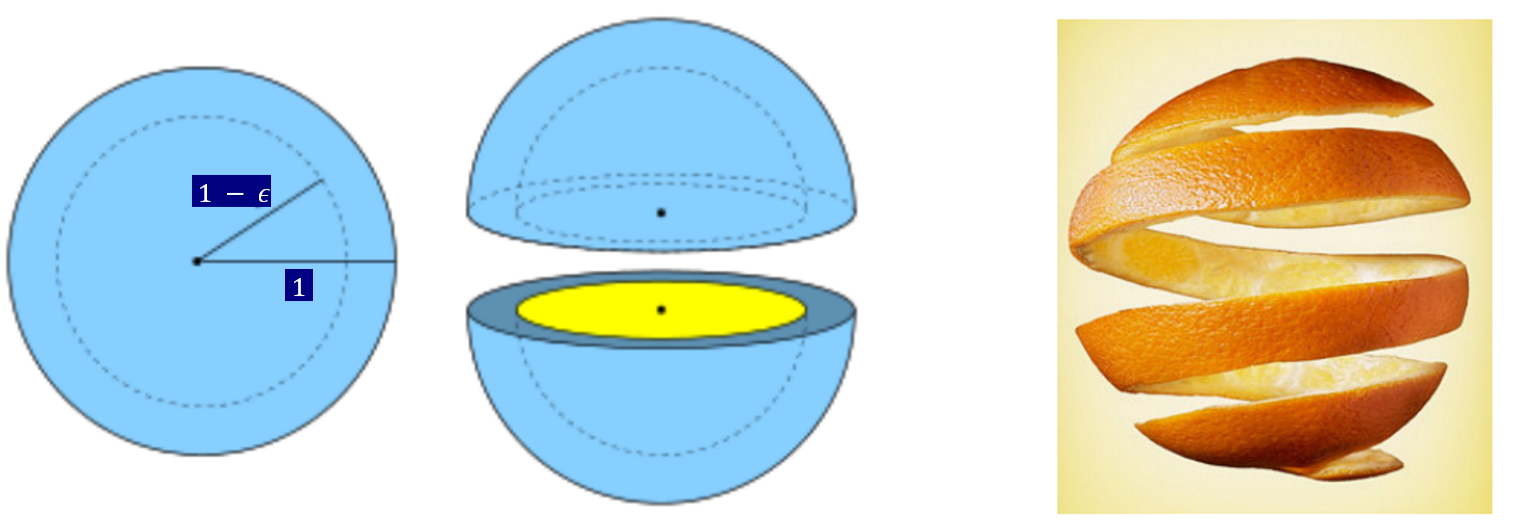
The ratio of the volume of a sphere of radius to one with unit raduis is,
This ratio as . So in high dimensions, all of the volume of the sphere is concentrated in a narrow annulus at the surface.
Cube
Consider a dimensional cube with unit-length sides centered at the origin.
- As increases, the volume remains constant at .
- However, the maximum distant between points, i.e. from one vertex to another, keeps increasing as . Eg. the distance between the vertex at and is
This is in interesting contrast to what we saw of the dimensional sphere of unit radius we saw earlier where,
- As increases the volume , and
- The maximum distance between two points given by the diameter remains constant at .
The relationship between the unit-length hypercube and unit-radius hypersphere as increases is shown below.
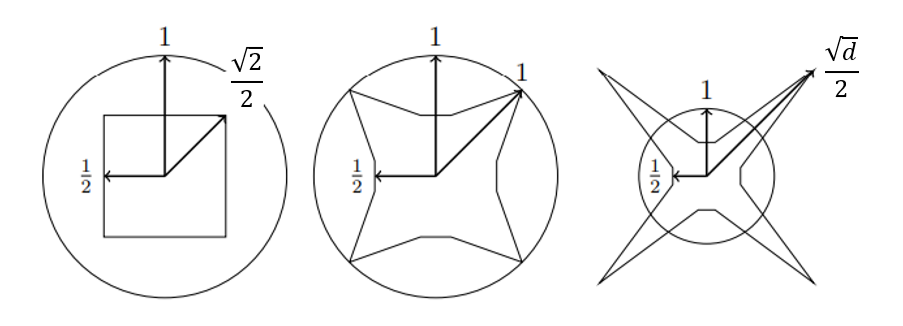
For , the cube is completely inside the sphere. Distance from origin to a vertex
For , the vertices of the cube lies exactly on the boundary of the sphere since the distance of from the origin to a vertex of the cube=
For any higher dimensions, the vertices of the cube exceed the confines of the sphere! However, there are still points of the cube that remain within the sphere (eg. ). So the high dimensional hypercube ends up with a “spiky” shape with distance from origin to a vertex=
Other weird stuff
- Most of the volume is within a narrow O(1/d) annulus
- Most of the volume is concentrated about the equator, defined as

Gaussians
For a d-dimensional spherical Gaussian of variance 1 , all but fraction of its mass is within the annulus for any
separation is required to separate means of d-dimensional spherical Gaussian of variance 1.